De Morgan azonosságok

Mi a De Morgan azonosság?

A De Morgan azonosságok két alapvető halmazelméleti szabály, amelyek leírják, hogyan viselkednek az unió és metszet műveletek, amikor komplementert képezünk.

Az azonosságok formulái

Első azonosság (unió komplementere):

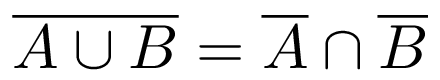
Vagyis: két halmaz uniójának komplementere megegyezik a komplementerek metszetével.

Második azonosság (metszet komplementere):

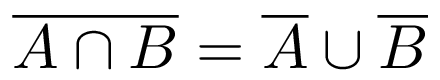
Vagyis: két halmaz metszetének komplementere megegyezik a komplementerek uniójával.

Venn-diagramos bizonyítás

Alapfogalmak

• Venn-diagram: körökkel ábrázoljuk a halmazokat
• A halmaz: az egyik kör
• B halmaz: a másik kör
• U (alaphalmaz): a teljes ábrázolandó univerzum

Első azonosság szemléltetése

Bal oldal vizsgálata:

• Az A ∪ B (unió): mindkét kör teljes területe (a „két egymásba harapott holdacska”)
• Az (A ∪ B)’: minden, ami ezen kívül esik az alaphalmazon belül

Jobb oldal vizsgálata:

• A’: minden, ami az A-n kívül van (az alaphalmaz többi része)
• B’: minden, ami a B-n kívül van (az alaphalmaz többi része)
• A’ ∩ B’: az a terület, amely mindkét komplementerben benne van

Színezéses módszer

• Az A ∪ B komplementerét jelöljük egy színnel (pl. piros)
• Az A’ halmazt jelöljük másik színnel (pl. kék)
• A B’ halmazt jelöljük harmadik színnel (pl. zöld)
• A metszet (A’ ∩ B’) ott van, ahol mindkét szín megjelenik

Eredmény: A két oldal ugyanazt a területet jelöli ki, ezzel bebizonyítottuk az azonosságot.

Gyakorlati alkalmazás

Mikor használjuk?

• Halmazelméleti kifejezések egyszerűsítése: komplementerek átalakítása
• Matematikai bizonyítások: tagadások kezelése
• Logikai műveletek: ÉS és VAGY kapcsolatok tagadása
• Informatika: logikai kifejezések optimalizálása

Matematikai logikában

A De Morgan azonosságok a logikában is érvényesek:

• nem (A és B) = (nem A) vagy (nem B)
• nem (A vagy B) = (nem A) és (nem B)

Kulcsfontosságú kapcsolatok

• Az unió és a metszet műveletek “felcserélődnek” komplementálás esetén
• A komplementer művelet megfordítja a halmazműveletek típusát:
• Unió → Metszet
• Metszet → Unió

Jelölések

• A’ vagy Ā: az A halmaz komplementere
• A ∪ B: A és B uniója
• A ∩ B: A és B metszete
• U: alaphalmaz (univerzum)

Megjegyzések

• A Venn-diagram szemléletes eszköz a bizonyításra
• A De Morgan azonosságok bármilyen halmazra érvényesek
• Alapvető eszközök a halmazelmélet és matematikai logika területén